Análisis inferencial

test de Chi cuadrado

El test de Chi2 nos permite saber si las varaibles son independientes entre si.

Si bien R no nos da como resultado una tabla tan completa como SPSS, es útil si únicamente queremos saber el resultado del test.

Por ejemplo, quiero saber si las varaibles “egoísmo” y “confianza” son independientes.

chisq.test(e3207$P26, e3207$P27)


    Pearson's Chi-squared test

data:  e3207$P26 and e3207$P27
X-squared = 1919.2, df = 100, p-value < 2.2e-16

Sin embargo, dado que en R todo lo que se genera son objetos, podemos explorar el “objeto” creado por el chisq.test()

z <- chisq.test(e3207$P26, e3207$P27)

Allí podemos observar los residuos, valores esperados, y residuos estandarizados.

View(z)

ANOVA

ANOVA nos sirve para saber si las diferencias en las medias entre grupos son diferentes respecto a una variable de interés.

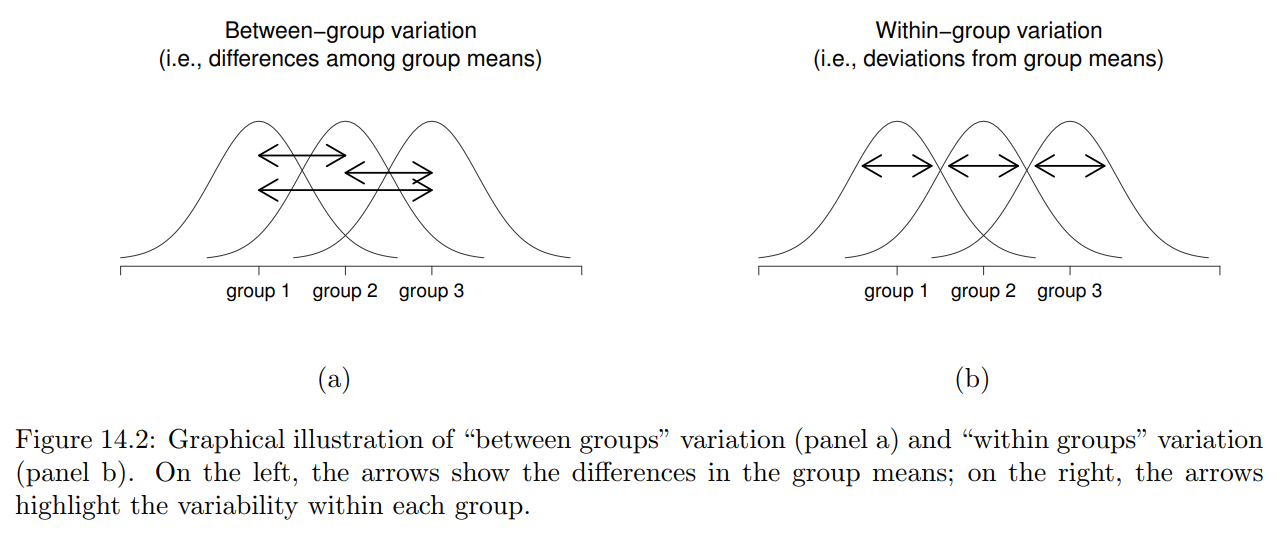
Por ejemplo, podemos estar interesados en conocer si el “buenrollismo” es diferente según la edad de las personas.

Podemos realizar este análisis en R con la función aov(). Es importante saber qué argumantos requiere la función. Para ello primero consultamos a R: ?aov

como podmeos ver, la función requiere que indiquemos la fórmiula, es decir las variables que queremos testear, y los datos que vamos a usar.

La fórmula se compone en su lado izquierdo por la variable “dependiente”, es decir, en nuestro caso, el “buenrollismo”, y en el lado derecho la variable independiente, es decir, los grupos etarios.

anova.br <- aov(br ~ edad4, data = e3207)

summary(anova.br)

              Df Sum Sq Mean Sq F value   Pr(>F)    
edad4          3    293   97.53   6.589 0.000197 ***
Residuals   2434  36028   14.80                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
28 observations deleted due to missingness

El resultado nos muestra los elementos principales del análisis de varianza: grados de libertad (df), suma de cuadrados, media cuadrática, el valor del F-test y el nivel de significación.

Regresión lineal

A diferencia de los anteriores procedimientos, la regresión lineal implica que las varaibles dependiente e independientes sean de nivel intervalar.

La idea central es saber cual es la razón de cambio en la variable dependiente cuando aumenta una unidad en la variable independiente.

Si relacionamos nuestras variables que componen “buenrollismo” podemos ver que están relacionadas.

Al igual que en ANOVA, R tiene una función integrada que nos permite realizar regresiones. En el caso de la regresión lineal es lm().

Los argumentos de esta función son los mismos que los de aov(), es decir, formula y data.

En clase queríamos saber si el “buenrollismo” causa felicidad. Dado que ambas variables son de nivel intervalar, podemos realizar un análisis de regresión.

feliz <- lm(P29 ~ br, data = e3207)

summary(feliz)


Call:
lm(formula = P29 ~ br, data = e3207)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.8014 -0.8014  0.2593  1.1379  2.9878 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 7.012228   0.086927  80.668  < 2e-16 ***
br          0.060706   0.008654   7.015 2.98e-12 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.642 on 2421 degrees of freedom
  (43 observations deleted due to missingness)
Multiple R-squared:  0.01992,   Adjusted R-squared:  0.01951 
F-statistic: 49.21 on 1 and 2421 DF,  p-value: 2.98e-12

qué obseramos aquí?

podemos observar los valores estimados para la variable dependiente cuando nuestra variable independiente está en 0.
el estimado del efecto de la variable independiente sobre la dependiente
el nivel de significación del efecto de la variable independiente.
el “ajuste” del modelo.