library(tidyverse)
library(haven)
e3207 <- read_sav("3207.sav")Anatomía de una Regresión
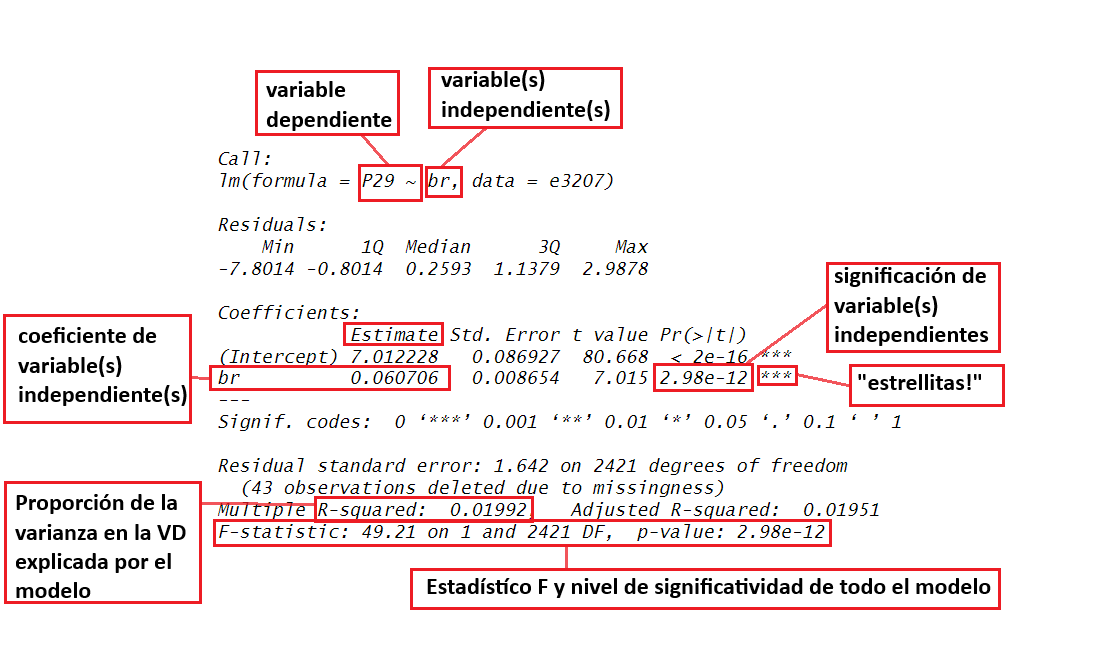
Fórmula regresión lineal
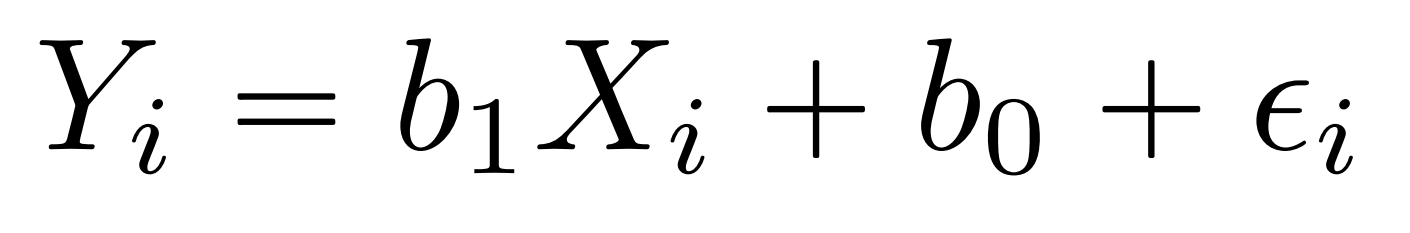
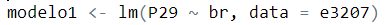
Fórmula regresión múltiple
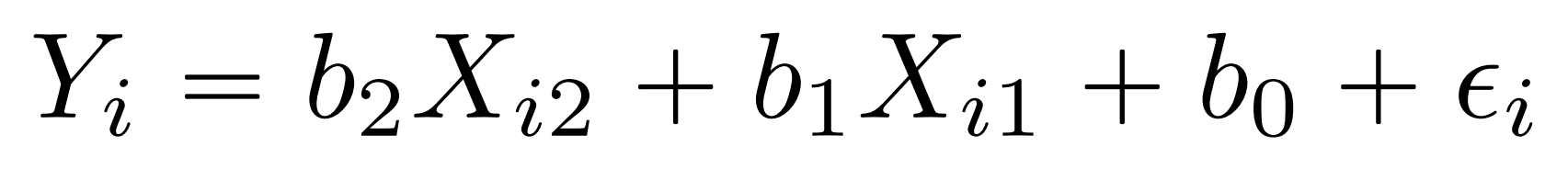
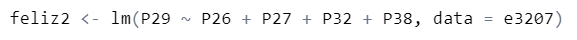
implementación en R
importamos nuestros datos y “llamamos” a las librerías que necesitamos.
Resolvemos los datos perdidos de las preguntas que nos interesan con na_if
e3207$P26 <- na_if(e3207$P26, 98)
e3207$P26 <- na_if(e3207$P26, 99)
e3207$P27 <- na_if(e3207$P27, 98)
e3207$P27 <- na_if(e3207$P27, 99)
e3207$P29 <- na_if(e3207$P29, 98)
e3207$P29 <- na_if(e3207$P29, 99)
e3207$P32 <- na_if(e3207$P32, 98)
e3207$P32 <- na_if(e3207$P32, 99)
e3207$P38 <- na_if(e3207$P38, 8)
e3207$P38 <- na_if(e3207$P38, 9)Finalmente implementamos un modelo de regresión lineal múltiple:
feliz <- lm(P29 ~ P26 + P27 + P32 + P38, data = e3207)
summary(feliz)
Call:
lm(formula = P29 ~ P26 + P27 + P32 + P38, data = e3207)
Residuals:
Min 1Q Median 3Q Max
-7.9721 -0.9098 0.0598 0.9403 3.7041
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.239803 0.196548 41.923 < 2e-16 ***
P26 0.087666 0.018263 4.800 1.71e-06 ***
P27 -0.001063 0.018505 -0.057 0.95421
P32 0.059780 0.018849 3.171 0.00154 **
P38 -0.499292 0.046656 -10.701 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.525 on 1870 degrees of freedom
(591 observations deleted due to missingness)
Multiple R-squared: 0.08539, Adjusted R-squared: 0.08343
F-statistic: 43.65 on 4 and 1870 DF, p-value: < 2.2e-16